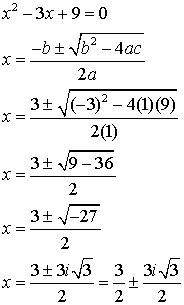Solving Quadratic Equations


Using the graphing calculator to find the solutions (roots) of quadratic equations.
We will look at using some basic graphing features to solve quadratic equations.
Keep in mind that the solutions might be TWO real numbers, ONE real number repeated,
or TWO complex numbers (complex conjugates).

There are special features for solving quadratic equations listed under Algebra 2.

Consider the following examples.

Using Graphing Features:

1. Using the ZERO Option
 

Solve:  x2 - 5x - 14 = 0

Since this equation is set equal to zero, the roots will be the locations where the graph crosses the x-axis (if the roots are real numbers).
(Remember that the x-axis is really just  y = 0.)

Start a new Document: Graph

1. Graph f1(x) = x2 - 5x - 14

2.  Use the ZERO option:
#6 Analyze Graph, #1 Zero
3.  Scroll (not arrow) the pointing hand, , to the left of one of the roots, click, , to lock the location. This will be called the "lower bound".
Now scroll to the right of the root, click to lock the location ("upper bound"). The root's coordinates (-2,0) will appear.
4. Repeat for the second root.
5. Answer:  zeros of the graph are at (-2,0) and (7,0)
So, the roots of the equation are x = -2, and x = 7.

 

2.
Using the INTERSECT Option
 
Solve:  2x2 + 2x = 7x - 2

Since this equation is NOT set equal to zero, the ZERO option cannot be used to look for roots(unless you re-write the equation so that it IS set equal to zero).

If you do not want to re-write the equation, solve using the intersect command to find the points where the two expressions intersect (if the roots are real numbers):

You may need to adjust the window to view both intersection points.

Start a new Document: Graph

1.  Set f 1(x) = 2x2 + 2x  and   f 2(x) = 7x - 2
2. Use the intersect option to find the roots.
#6 Analyze Graph, #4 Intersection
3.  Scroll the pointing hand, , to the left of one of the intersection points, click, , to lock the location.
Now scroll to the right of the intersection point, click to lock the location. The intersection's coordinates (0.5,1.5) will appear.
4. Repeat for the second intersection point.
5. Answer: At x = 0.5 and x = 2, both graphs have the same y-values, thus making these points the solutions where the graphs equal one another.
ANSWER: x = 0.5, and x = 2.
Window [-3,3] x [-5,15]

 

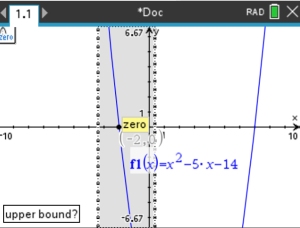
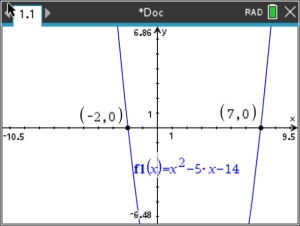
3.
Using a GEOMETRY Option for Intersection
 
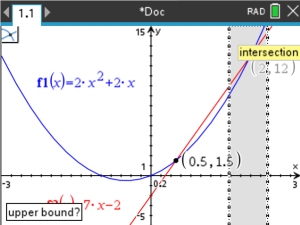
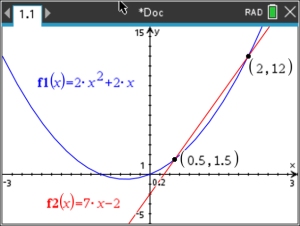
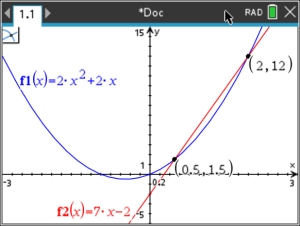
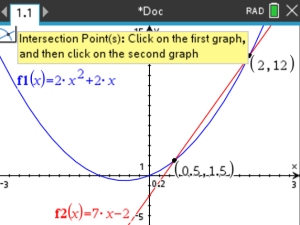
Solve:  2x2 + 2x = 7x - 2

Let's try the equation from Example 2 again.

This time we will use a Geometry option.
Start a new Document: Graph

1.  Prepare the graph,
Set f 1(x) = 2x2 + 2x  and   f 2(x) = 7x - 2

2. #8 Geometry, #1 Points & Lines,
#4 Intersection Points

3.  Click on BOTH graphs.

4. Both intersection points will appear with their coordinates.
  ANSWER: x = 0.5, and x = 2.

Note: If you forget what to do after step 3, click on the symbol in the upper left corner of the screen, and a hint will drop down (in yellow).
Window [-3,3] x [-5,15]

 

4.
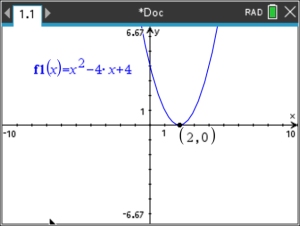
Only One Root?

 

 

 
Solve:  x2 - 4x + 4 = 0

When graphed, this equation only intersects the x-axis in one location.  This tells you that this root repeats itself.   

Follow the process using the Zero option described in Example 1 to officially identify the point as a zero.

ANSWER: x = 2 repeated

 

5.
What if the graph does not intersect the x-axis???
(or intersect option shows no intersections)
 
Solve:  x2 - 3x + 9 = 0

Start a new Document: Graph

When graphed, this equation does NOT intersect the x-axis.  This tells you that the roots of this equation are complex (imaginary) values. 

The first solution would be to dig out the quadratic formula. as shown below.

Using quadratic formula to find the roots.

solved 1
Window [-5,5] x [-5,15]

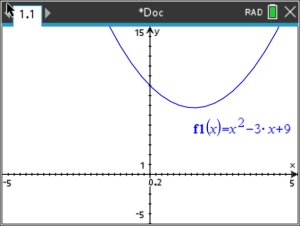Remember that complex roots come in conjugate pairs.

There is a special feature for solving quadratic equations that can be seen under Algebra 2.

 

 

 

divider
Table of Contents | MathBits.com | Terms of Use
Table of Contents MathBits.com Terms of Use TI-84+ web site